二叉查找树 BST

Posted on | In |

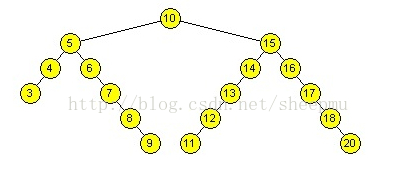
BST特点

在二叉查找树中：
(1) 若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；

(2) 任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；

(3) 任意节点的左、右子树也分别为二叉查找树。

(4) 没有键值相等的节点（no duplicate nodes）。

找前驱和后继节点

BST中某节点前驱节点==小于该节点的所有节点中的最大值

前驱容易情形：5寻前驱 4

前驱复杂情形：11寻前驱 10

BST中某节点后继节点==大于该节点的所有节点中的最小值
后继容易情形：5寻后继 6

复杂情形：9寻后继 10

image

二叉树的插入

a.若当前的二叉查找树为空，则插入的元素为根节点

b.若插入的元素值小于根节点值，则将元素插入到左子树中

c.若插入的元素值不小于根节点值，则将元素插入到右子树中。首先找到插入的位置，要么向左，要么向右，直到找到空结点，即为插入位置，如果找到了相同值的结点，插入失败。

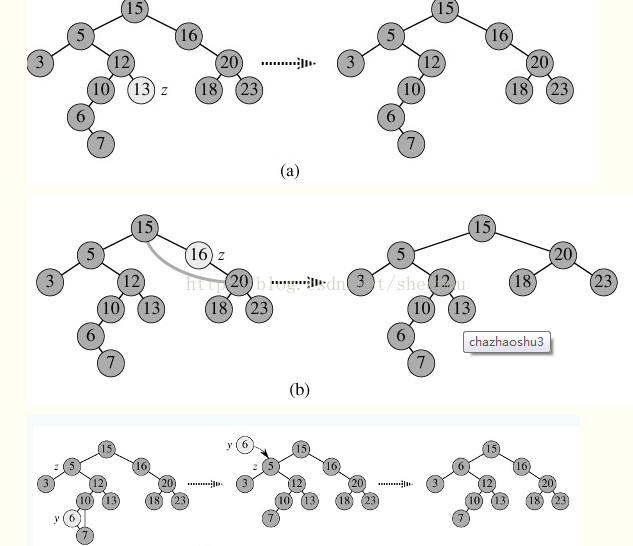
二叉查找树的删除

分三种情况进行处理：

1.p为叶子节点，直接删除该节点，再修改其父节点的指针（注意分是根节点和不是根节点），如图a。

2.p为单支节点（即只有左子树或右子树）。让p的子树与p的父亲节点相连，删除p即可；（注意分是根节点和不是根节点）；如图b。

3.有两个孩子的情况，当前结点与左子树中最大的元素交换，然后删除当前结点。左子树最大的元素一定是叶子结点，交换后，当前结点即为叶子结点，删除参考没有孩子的情况。另一种方法是，当前结点与右子树中最小的元素交换，然后删除当前结点。如图c。
image

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156

class TreeNode {
	int value;
	TreeNode parent;
	TreeNode left;
	TreeNode right;

	public TreeNode(int value, TreeNode parent, TreeNode left, TreeNode right) {
		this.value = value;
		this.parent = parent;
		this.left = left;
		this.right = right;
	}
}

public class BST {
	public TreeNode getMax(TreeNode root) {
		if (root == null)
			return null;
		while (root.right != null)
			root = root.right;
		return root;
	}

	public TreeNode getMin(TreeNode root) {
		if (root == null)
			return null;
		while (root.left != null)
			root = root.left;
		return root;
	}

	public TreeNode search(TreeNode root, int val) {
		if (root == null)
			return root;
		if (root.value < val)
			return search(root.left, val);
		else if (root.value > val)
			return search(root.right, val);
		else
			return root;
	}

	public TreeNode preNode(TreeNode x) {
		if (x.left != null)
			return getMax(x.left);
		// 如果x没有左孩子。则x有以下两种可能：
		// (01) x是"一个右孩子"，则"x的前驱结点"为 "它的父结点"。
		// (02) x是"一个左孩子"，则 前驱节点为x的某一个祖先节点的父节点，而且该祖先节点是作为其父节点的右儿子
		else {
			TreeNode p = x.parent;
			while (p != null && p.left == x) {
				x = p;
				p = p.parent;
			}
			return p;
		}
	}

	public TreeNode postNode(TreeNode x) {
		if (x.right != null)
			return getMin(x.right);
		// 如果x没有左孩子。则x有以下两种可能：
		// (01) x是"一个右孩子"，则"x的前驱结点"为 "它的父结点"。
		// (02) x是"一个左孩子"，则 前驱节点为x的某一个祖先节点的父节点，而且该祖先节点是作为其父节点的左儿子
		else {
			TreeNode p = x.parent;
			while (p != null && p.right == x) {
				x = p;
				p = p.parent;
			}
			return p;

		}
	}

	public TreeNode insertRec(TreeNode root, TreeNode x) {
		if (root == null)
			root = x;
		else if (x.value < root.value)
			root.left = insertRec(root.left, x);
		else if (x.value > root.value)
			root.right = insertRec(root.right, x);
		return root;
	}

	public void delete(TreeNode root, TreeNode x) {
		if (root == null)
			return;
		TreeNode p = null;
		while (root != null)// 定位到需要删除的节点
		{
			if (x.value < root.value) {
				p = root;// 记录父节点
				root = root.left;
			} else if (x.value > root.value) {
				p = root;// 记录父节点
				root = root.right;
			} else// 找到啦
			{
				if (root.left == null && root.right == null)// ①待删除的是 叶子节点
				{
					if (p == null)// 待删除的是根节点
						root = null;
					else {
						if (p.left == root)
							p.left = null;
						else if (p.right == root)
							p.right = null;
					}
				} else if (root.left != null && root.right == null)// ②
																	// 待删除的节点只有左孩子
				{
					if (p == null)// 待删除的是根节点
						root = root.left;
					else {
						if (p.left == root)// 待删除的本身是一个左孩子
							p.left = root.left;
						else if (p.right == root)
							p.right = root.left;
					}
				} else if (root.left == null && root.right != null)// ②
																	// 待删除的节点只有右孩子
				{
					if (p == null)// 待删除的是根节点
						root = root.right;
					else {
						if (p.left == root)// 待删除的本身是一个左孩子
							p.left = root.right;
						else if (p.right == root)
							p.right = root.right;

					}
				} else// ③待删除的节点即有左孩子又有右孩子 方法：得到待删除节点右子树的最小值，
				{// 该最小值与待删除节点进行“ 值 ”交换，删除该最小值位置处的节点
					TreeNode rMin = root.right; // 求待删除节点的后继节点,即待删除节点的右孩子的最小值(找到的后继节点肯定没有左孩子！！！)
					TreeNode rMinP = null;// 因为需要删除后继节点位置，所以需要记录父节点
					while (rMin != null) {
						rMinP = rMin;
						rMin = rMin.left;
					}
					int rootVtemp = root.value;// 值交换
					root.value = rMin.value;
					rMin.value = rootVtemp;
					// 删除rMin位置的节点，此时此位置的值已是待删节点的值
					if (rMinP.left == rMin)
						rMinP.left = rMin.right;
					else if (rMinP.right == rMin)
						rMinP.right = rMin.right;
				}
			}
			break;// 找到后删了后就跳出while循环
		}

	}
}