leetcode 787. Cheapest Flights Within K Stops

Posted on | In |

There are n cities connected by m flights. Each fight starts from city u and arrives at v with a price w.

Now given all the cities and flights, together with starting city src and the destination dst, your task is to find the cheapest price from src to dst with up to k stops. If there is no such route, output -1.

Example 1:
Input:

n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]]

src = 0, dst = 2, k = 1

Output: 200

Explanation:
The graph looks like this: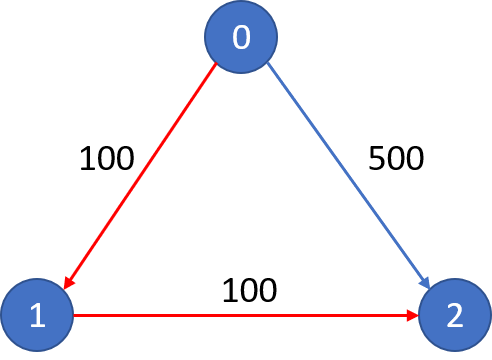
image
The cheapest price from city 0 to city 2 with at most 1 stop costs 200, as marked red in the picture.

Example 2:

Input:

n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]]

src = 0, dst = 2, k = 0

Output: 500

Explanation:

The graph looks like this:

image

The cheapest price from city 0 to city 2 with at most 0 stop costs 500, as marked blue in the picture.

Note:

The number of nodes n will be in range [1, 100], with nodes labeled from 0 to n - 1.

The size of flights will be in range [0, n * (n - 1) / 2].

The format of each flight will be (src, dst, price).

The price of each flight will be in the range [1, 10000].
k is in the range of [0, n - 1].

There will not be any duplicated flights or self cycles.

bfs剪枝

最优化剪枝

从src 到 dst可能有多条路径

把走一步的节点加进来，统计step数 如果大于k break

累积到当前节点的cost大于记录下的ans 就跳过

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
struct node{
    int num;
    int cost;
    node(int nn,int cc){
        num=nn;
        cost=cc;
    }
};
class Solution {
public:
    map<int,vector<node> >g;
    int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int K) {
        for(int i=0;i<flights.size();i++){
                g[flights[i][0]].push_back(node(flights[i][1],flights[i][2]));
        }
        int ans=1e8;
         bfs(src,dst,ans,K); 
        if(ans==1e8) return -1;
        else return ans; 
    }
    

    void bfs(int src,int dst,int &ans,int k){   
        queue<node> q;
        int cost=0;
        q.push(node(src,0));
        int step=0;
        while(!q.empty()){
            int size=q.size();

            while(size--){
                node t=q.front();
                q.pop();
                if(t.num==dst) {
                    ans=min(ans,t.cost);
                }
                //访问过的节点还能访问 k步以内即可
                //  if(vis[t.num]) continue;
                // vis[t.num]=true;!!
                 cost=t.cost;
            for(int i=0;i<g[t.num].size();i++){
                node  b=g[t.num][i];
              if(cost+b.cost>ans) continue;
                q.push(node(b.num,cost+b.cost));
                
            }
                  
            }
         if(step++>k) break;
           
             
     }
   
        
    }
};

dfs 剪枝

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

struct node{
    int num;
    int cost;
    node(int nn,int cc){
        num=nn;
        cost=cc;
    }
};
class Solution {
public:
    map<int,vector<node> >g;
    int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int K) {
        for(int i=0;i<flights.size();i++){
                g[flights[i][0]].push_back(node(flights[i][1],flights[i][2]));
        }
        bool vis[101]={false}; 
        int cost=0,ans=1e8;
         dfs(src,dst,vis,K+1,ans,cost); 
        if(ans==1e8) return -1;
        else return ans;
    }
    
    
    void dfs(int src,int dst,bool vis[],int k,int &ans,int cost){   
       if(src==dst) {
           ans=cost;
           return;
       }
        if(k==0) return;
        for(int i=0;i<g[src].size();i++){
            if(vis[g[src][i].num]) continue;

            if(g[src][i].cost+cost>ans) continue;
                    vis[g[src][i].num]=true;
            dfs(g[src][i].num,dst,vis,k-1,ans,cost+g[src][i].cost);
                vis[g[src][i].num]=false;
        }
        
        
    }
};