凸多边形的最优三角划分

Posted on | In |

问题相关定义：

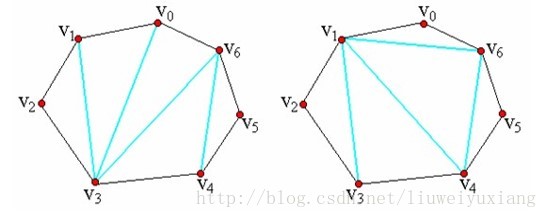
(1)凸多边形的三角剖分：将凸多边形分割成互不相交的三角形的弦的集合T。

(2)最优剖分：给定凸多边形P，以及定义在由多边形的边和弦组成的三角形上的权函数w。要求确定该凸多边形的三角剖分，使得该三角剖分中诸三角形上权之和为最小。

凸多边形三角剖分如下图所示：
image

设m[i][j]，1<=i < j<=n 为凸多边形{Vi-1,Vi……Vj}的最优三角剖分所对应的权值函数值，即其最优值。最优剖分包含三角形Vi-1VkVj的权，子多边形{Vi-1,Vi……Vk}的权，子多边形{Vk，Vk+1……Vj}的权之和。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include<bits/stdc++.h>
#define MAX 100
int s[MAX][MAX],m[MAX][MAX],g[MAX][MAX];
int n;
using namespace std;
//点i-1 i.....j构成的凸多边形的划分 
void print(int i,int j){
	if(i==j) return;
	//i-1--->s[i][j]是弦 不是边 
	if(s[i][j]>i) {
		cout<<"{v"<<i-1<<" v"<<s[i][j]<<"}"<<endl; 
	}
	//s[i][j]--->j是弦 不是边 
	if(s[i][j]+1<j){
		cout<<"{v"<<s[i][j]<<" v"<<j<<"}"<<endl;
	}
	print(i,s[i][j]);
	print(s[i][j]+1,j);
	
}
int main(){
	cin>>n;
	n--;
	for(int i=0;i<=n;i++){
		for(int j=0;j<=n;j++){
			cin>>g[i][j];
		}
		
	}
	for(int d=2;d<=n;d++)
	{
		for(int i=1;i<=n+d-1;i++){
			int j=i+d-1;
			m[i][j]=m[i+1][j]+g[i-1][i]+g[i][j]+g[i-1][j];
			s[i][j]=i;
			for(int k=i+1;k<j;k++){
				if(m[i][j]>m[i][k]+m[k+1][j]+g[i-1][k]+g[i-1][j]+g[k][j])
				{
					m[i][j]=m[i][k]+m[k+1][j]+g[i-1][k]+g[i-1][j]+g[k][j];
					s[i][j]=k;
				}
			}
			
		}
		
	}
	cout<<m[1][n]<<endl;
	print(1,n);
	return 0;
}

参考博客
https://blog.csdn.net/liuweiyuxiang/article/details/78827474