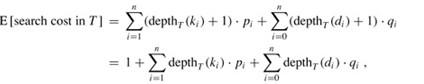最优二叉搜索树

Posted on | In |
  1. 概述
    　　利用最优二叉搜索树来实现树的搜索代价最小。树上的每一个节点都有一个被搜索到的概率值，搜索一个节点的花费为，如何构造一个二叉查找树使搜索树上的 所有节点的花费最小即为实现最优二叉查找树的问题。该问题可以用动态规划的思路实现。
    　　形式化定义：给定n个不同关键字已经排序的序列,我们希望用这些关键字构造一个二叉搜索树。对每个关键字,都有概率表示起搜索概率。有些要搜索的值可能不再K中，因此我们还需要n+1个伪关键字，对于每一个伪关键字都有一个概率表示对应的搜索概率。
  2. 问题案例
    　　n=5的关键字集合以及如下的搜索概率，构造二叉搜索树。

image

期望搜索代价的计算公式：
image

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
#include<bits/stdc++.h>
#define MAX 100
using namespace std;
//!
double p[MAX];
double q[MAX];
double w[MAX][MAX],c[MAX][MAX],s[MAX][MAX]; 
void print(int i,int j,int flag){
	if(flag==0){
		cout<<"root:"<<s[i][j]<<endl;
		flag=1;
	}
	int k=s[i][j];
	if(k>=i+1){
		cout<<"S"<<k-1<<"is the left child of"<<"S"<<k<<endl;
		print(i,k-1,1);
	}
	else{
			cout<<"E"<<i-1<<"is the left child of"<<"E"<<k<<endl;
	}
		if(k<j){
		cout<<"S"<<k+1<<"is the right child of"<<"S"<<k<<endl;
		print(k+1,j,1);
	}
	else{
			cout<<"E"<<k<<"is the right child of"<<"E"<<k<<endl;
	}
	
	
} 
int main(){
	int n;
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>p[i];
		
	}
	for(int i=0;i<=n;i++)
	cin>>q[i];
	for(int i=1;i<=n+1;i++)
	{
				w[i][i-1]=q[i-1];
				c[i][i-1]=0;
	}
	for(int d=1;d<=n;d++){
		for(int i=1;i<=n-d+1;i++)
		{
			int j=i+d-1;
			w[i][j]=w[i][j-1]+p[j]+q[j];
			double tmp=c[i+1][j]+w[i][j];//保存i-j构成二叉搜索树查找次数的最小值 
				s[i][j]=i;
				for(int k=i+1;k<=j;k++){
					if(c[i][k-1]+c[k+1][j]+w[i][j]<tmp&&fabs(c[i][k-1]+c[k+1][j]+w[i][j]-tmp)>1e-6){
						tmp=c[i][k-1]+c[k+1][j]+w[i][j];
						s[i][j]=k;
					}
				}
				c[i][j]=tmp;
				
			
		}
		
		
	}
	cout<<c[1][n]<<endl;
	print(1,n,0);
	
}

image

參考博客

https://blog.csdn.net/zhangyifei521/article/details/50833792